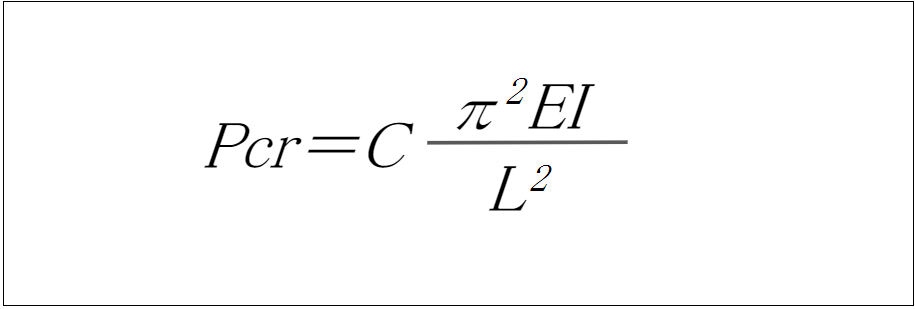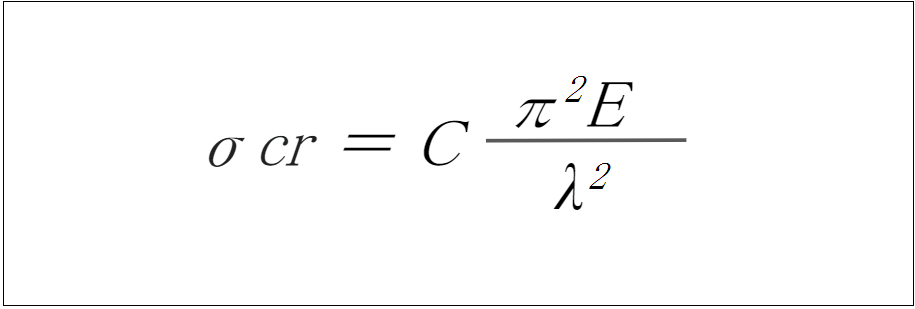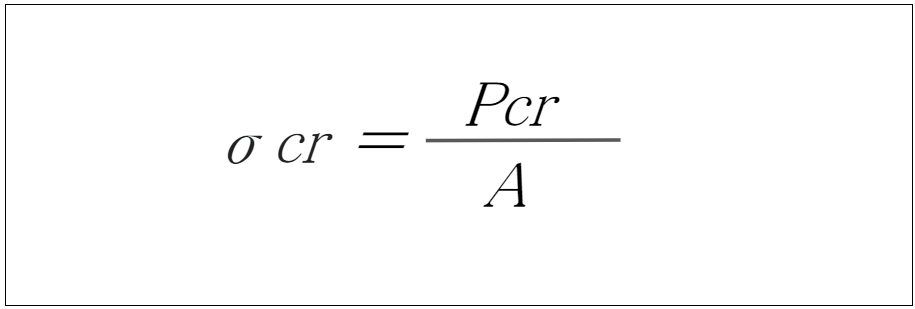今日は「座屈計算(荷重・応力)の計算式と必要な情報まとめ」についてのメモです。
私たち機械設計者が設計する機械は、結果的にコンパクトに纏められることが多いので、座屈荷重や座屈応力を確認する必要のある場所というのはあまり多くない気がしています。
しかし、機械内部で柱を持つ構造体を、上から押付けたりする場合(結果的に押付けられる場合)は、機械の押付け力に対して 支えている柱の座屈荷重・座屈応力は問題ないのか を確認する場合があります。
今日はその時に使える柱(軸)の座屈荷重の計算方法をメモしておきますが、座屈荷重の計算と座屈応力の計算は事前に理解しておく事がいくつかあるので
- 始めに「座屈荷重」についての基本事項まとめ
- 次に「座屈応力」についての基本事項まとめ
- 座屈荷重及び座屈応力の公式の説明
- 座屈荷重及び座屈応力の公式
- 最後に。計算書のダウンロード
という流れで進めていきたいと思います。
座屈とは?座屈に関する計算式と必要な情報
始めに「座屈荷重」についての基本事項まとめ
座屈とは 柱や軸の上から負荷を掛けた時に折れ曲がる現象 ですが、その 座屈が起きる時の荷重を座屈荷重 といい、座屈したとき材料に掛かる圧縮応力度を座屈応力 といいます。
座屈には一般的に
- 太い柱や軸:座屈荷重が高い(座屈しにくい)
- 短い柱や軸:座屈荷重が高い(座屈しにくい)
- 細い柱や軸:座屈荷重が低い(座屈しやすい)
- 長い柱や軸:座屈荷重が低い(座屈しやすい)
と言えますが、具体的には以下の要素4つが影響しています。
①形状の持つ特性:断面二次モーメント
断面二次モーメントは 曲げる力に対する部材の変形のしにくさを表した断面の特性 で、断面二次モーメントが値が高い形状は座屈しにくいが、低い形状は座屈しやすい。
②支点間の距離:座屈長さ
座屈長さが短い柱は座屈しにくいが、長い柱は座屈しやすい。
③材料の持つ特性:縦弾性係数
弾性係数が高い材料は座屈しにくいが、低い材料は座屈しやすい。縦弾性係数はヤング率とも呼ばれる材料の物性値です。
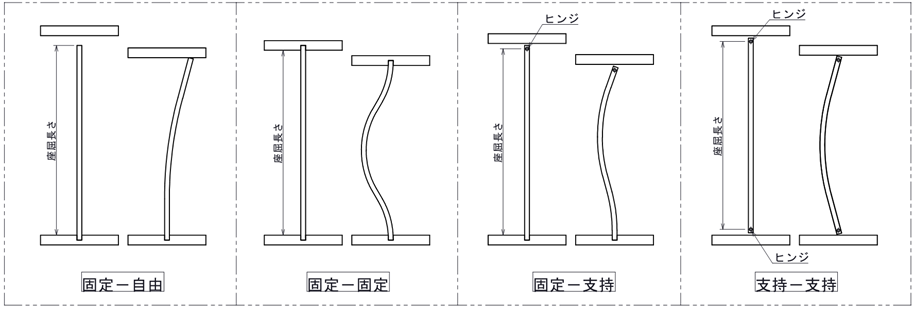
④固定方法による違い:端末条件係数
柱の上下末端の保持方法によって座屈しやすかったり、座屈しにくかったりが変わります。座屈荷重や座屈応力を求める際に、柱の境界条件(取り付け方法)が異なる場合は端末条件係数と呼ばれる値を設定しますが、その係数は次の値となります
- ヒンジ×ヒンジ:C = 1.0
- 固定×自由:C = 0.25
- 固定×ヒンジ:C = 2.046
- 固定×固定:C = 4
次に「座屈応力」についての基本事項まとめ
次に座屈応力ですが、座屈応力は柱(軸)の
- 細長比が大きい(細い柱)ほど座屈応力度は小さくなる
- 細長比が小さい(太い柱)ほど座屈応力度は大きくなる
といえます。応力とは物体に外力が加わる場合、それに応じて物体の内部に生ずる抵抗力。つまり、細長比が大きい(細い柱)ほど抵抗力が低いという事になります。
この細長比を求めるには、まず断面二次モーメントと断面積から断面二次半径を求め、座屈長さをこの断面二次半径で除し細長比を求めます。断面二次半径は、断面回転半径とも呼ばれ、この値が大きいほど座屈しにくなります。
但し、ここも柱の境界条件(取り付け方法)が異なる場合はたわみ形状が変化するため、座屈長さに有効長さ係数を掛け、有効細長比を求める事が必要です。
ヒンジ×ヒンジ:K = 1.0
固定×自由:K = 2.0
固定×ヒンジ:K = 0.7
固定×固定:K = 0.5
座屈荷重及び座屈応力の公式の説明
さて、ようやく座屈荷重を求める公式の説明に入ります。座屈荷重や座屈応力の公式は オイラーの式 利用します。
但し、このオイラーの式が適用になるには 細長比の限界以上であるかどうかの確認が必要 となります。その理由は、オイラーの式は座屈荷重に達するまでに、柱に生じる応力は弾性限度内にあると仮定して導かれたものだからです。
短い柱は、弾性の座屈が起こる前に塑性変形が生じ、結果的に座屈応力はオイラーの式で求められる値よりも低くなりますので、材料の降伏点に対してオイラーの式が適用できる柱の長さ(細長比)の限界を知り、その値より大きい細長比に対しては上記のオイラーの式(座屈計算・座屈応力計算式)が適用されます。
つまり、座屈荷重を単純に計算しても、その式が適用できる状態のものかも確認しないといけません。
では、以下に座屈荷重と座屈応力の計算式をメモしていきます。(実際の計算は計算書をお使いください)
座屈荷重を求める計算式
- Pcr: 座屈荷重
- C: 端末条件係数
- E: 縦弾性係数(ヤング率)
- I: 断面2次モーメント
- L: 座屈長さ
座屈荷重が発生している時、断面積に掛かる座屈応力を求める計算式(その1)
- σcr: 座屈応力
- C: 端末条件係数
- E: 縦弾性係数(ヤング率)
- λ:柱の細長比(L/i)
- i:断面2次半径(i=√I/A)
座屈荷重が発生している時の断面積に掛かる座屈応力度を求める(その2)
座屈応力を求めるには以下の式でも構いません。
- σcr: 座屈応力
- Pcr: 座屈荷重
- A:断面積
ちょっと補足
これまで説明してきた座屈計算は基本的なものです。 建築に近い構造設計においては、今回記事にした単純な座屈とは別に
- ねじれながら横に倒れる横座屈
- 梁端部圧縮側のフランジが波をうつように座屈することを局部座屈
というものがあります。また、少し対処が難しそうな
- 分岐座屈
- 飛び移り座屈
というものもあります。今回記事にした単純な座屈(オイラー座屈)は、我々の設計する機械(真っ直ぐ動作するもの)に対しては有効な計算だと思いますが、建築物のような大型で骨組みが長い構造体を設計する際には、横座屈や局部座屈に考慮が必要だと考えています。
もちろん、機械は内部で機器が動くため、結果的に合成の高い構造体になる事が殆どだと思うのですが、
- もし横座屈に考慮が必要な場合は横補鋼材(横方向の補強)で横座屈に対応
- 局部座屈に考慮が必要な場合は幅厚比を変えることで局部座屈に対応
という意識を持つと良いと思います。
最後に。計算書のダウンロード
ここでは座屈荷重の計算書と、座屈応力の計算緒をダウンロードしていただけます。(フリーソフトですのでご自由にお使いください)
また、鋼材を座屈荷重計算の対象にすることもあるかと思います。当ブログでは現在1点、座屈計算に使える資料があります。
宜しければ、参照先のデータ内の 断面積(A)、断面二次モーメント(I)、断面二次半径(i)をお使いください
以上です。
-

-
基本計算
設計計算 ここでは、私が実務で利用している 機械設計における基本計算をメモ しております。 計算書が付いている記事や計算書は随時改訂しておりますので利用される場合は最新版をご利用下さい。 また、何か間 ...
続きを見る