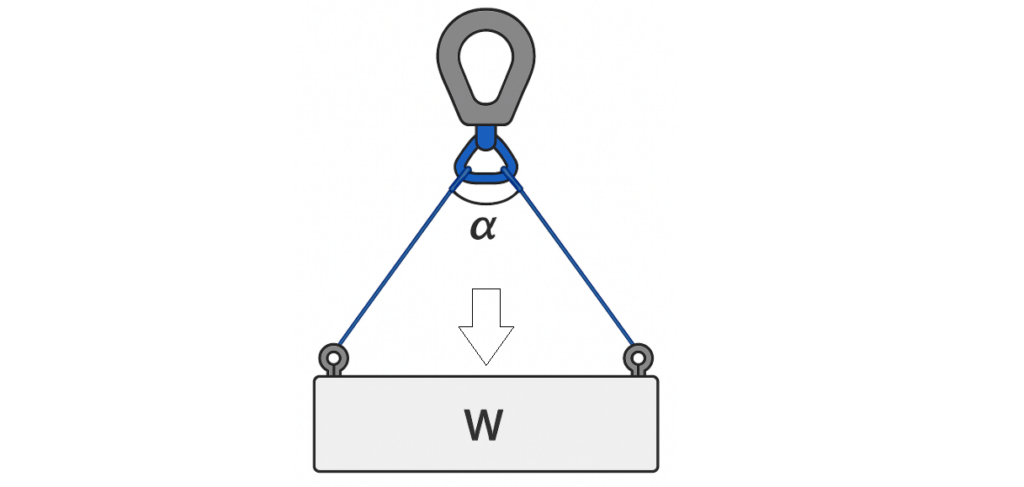
ここでは「吊り角度による張力の計算方法」をメモしています。 この計算はアイボルトなどで重量物を吊る際に掛かるワイヤーへの張力などに応用できます。
吊角度による張力の計算
吊り上げ対象物にアイボルトを 2個・3個・4個 取り付けて斜め吊りを行う場合、ワイヤー(スリング)にかかる引張荷重(張力) は、吊り角度(ワイヤーの傾き)によって大きく変わります。
斜めに吊ると、ワイヤー1本あたりにかかる荷重(張力)は、吊り角度(ワイヤー角度)が大きいほど大きくなる特性があります。 角度が広い場合、水平方向に強く引く必要があり、張力は増えます。 つまり、吊り荷重を複数のワイヤーで支える場合、
- ワイヤーが垂直に近いほど、張力は小さく済む。
- ワイヤーが水平に近いほど、張力は大きくなる。(より強いワイヤーが必要となる)
となります。
張力の計算式
T = W / (n × cosθ)
- T:ワイヤー1本にかかる張力(N または kgf)
- W:吊り上げ対象物の重さ(N または kgf)
- n:吊り点の数(ワイヤーの本数。2点吊りなら2、4点なら4)
- α:ワイヤーの角度
※計算では角度の部分で「cosθ」を使います。 α=30なら半分のcos15°、45ならcos22.5°となります。
具体例1
2点吊り、重さ1,000kg、吊り角度α30°=cos15°
- W = 1,000kg
- n = 2
- α = 30°(cos15°= 0.96593)
T = 1,000 / (2 × 0.96593) = 517kgf → ワイヤー1本に517kgfの張力が掛かる。
具体例2
2点吊り、重さ1,000kg、吊り角度α45°=cos22.5°
- W = 1,000kg
- n = 2
- α = 45°(cos22.5°= 0.92388)
T = 1,000 / (2 × 0.92388) = 541kgf → ワイヤー1本に541kgfの張力が掛かる。
具体例3
2点吊り、重さ1,000kg、吊り角度α60°=cos30°
- W = 1,000kg
- n = 2
- α = 60°(cos30° = 0.86603)
T = 1,000 / (2 × 0.86603) = 577kgf → ワイヤー1本に577kgfの張力が掛かる。
具体例4
4点吊り、重さ1,000kg、吊り角度α60°=cos30°
- W = 1,000kg
- n = 4
- α = 60°(cos30° = 0.86603)
T = 1,000 / (4 × 0.86603) = 288kgf → ワイヤー1本に288kgfの張力が掛かる。
※対象物の上面には計4本のワイヤーが等分に取り付けられている想定
※4点吊りで均等に荷重が掛かり難い場合、3点吊りにて計算をしてください。
参考値
θ = 15.0° → cos(15.0°) = 0.96593
θ = 17.5° → cos(17.5°) = 0.95372
θ = 20.0° → cos(20.0°) = 0.93969
θ = 22.5° → cos(22.5°) = 0.92388
θ = 25.0° → cos(25.0°) = 0.90631
θ = 27.5° → cos(27.5°) = 0.88701
θ = 30.0° → cos(30.0°) = 0.86603
θ = 32.5° → cos(32.5°) = 0.84339
θ = 35.0° → cos(35.0°) = 0.81915
θ = 37.5° → cos(37.5°) = 0.79335
θ = 40.0° → cos(40.0°) = 0.76604
θ = 42.5° → cos(42.5°) = 0.73728
θ = 45.0° → cos(45.0°) = 0.70711
注意
上記計算は掛かる張力の計算であり、使用するワイヤーの持つ破断強度は安全率を適切に掛けたものを利用してください。
以上です。